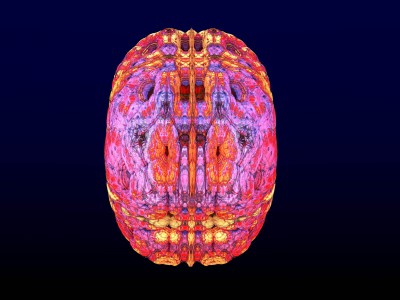
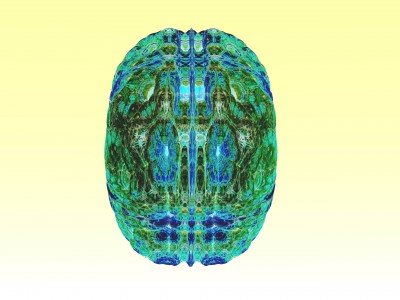
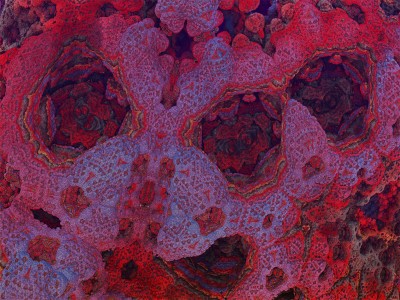
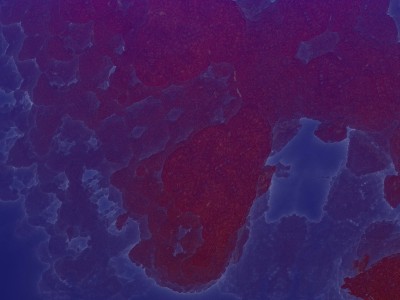
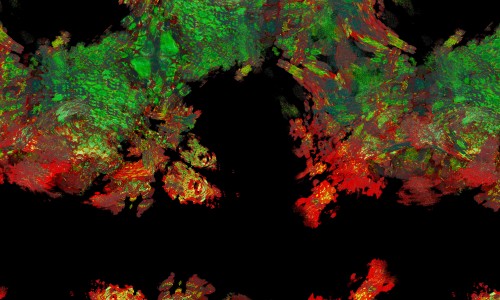
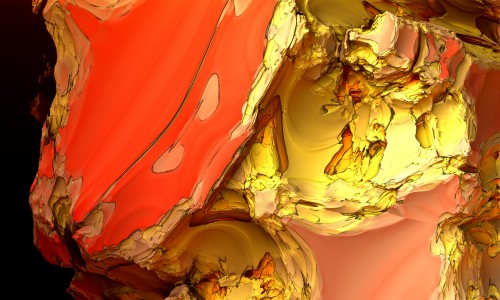
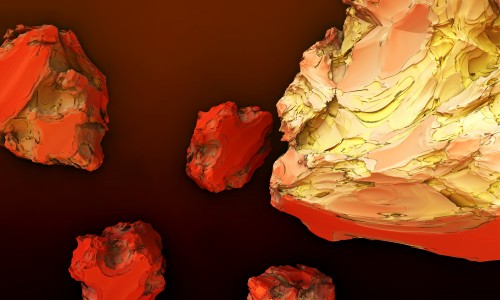
µN explore l’architecture invisible des nombres et des équations.
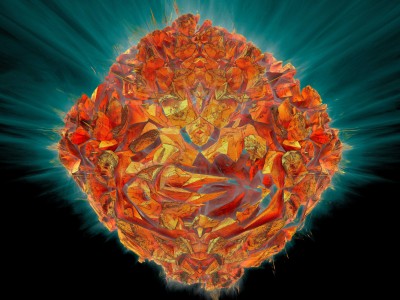
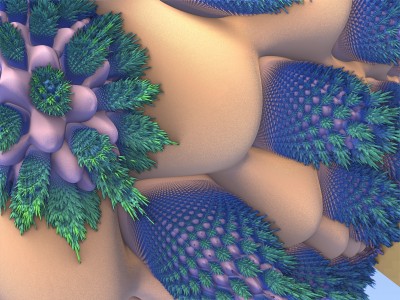
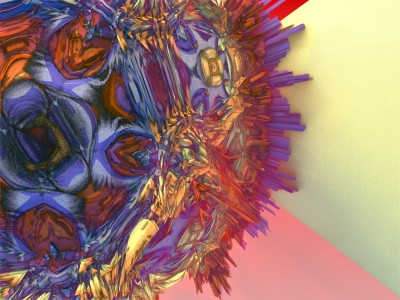
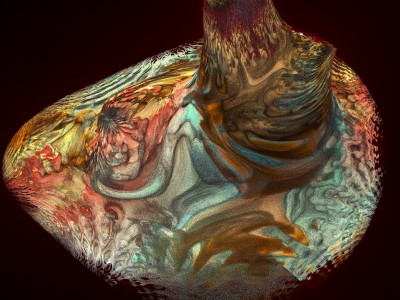
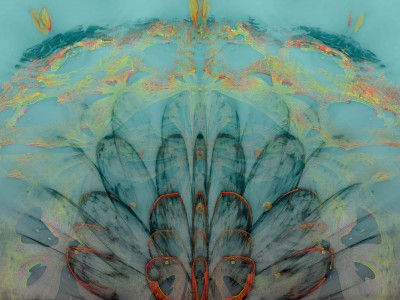
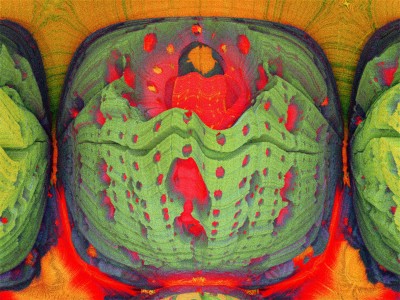
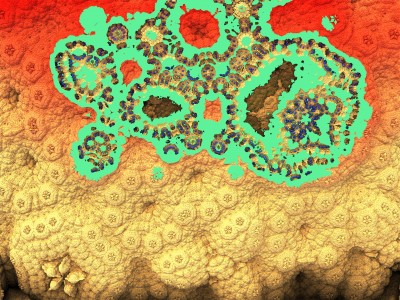
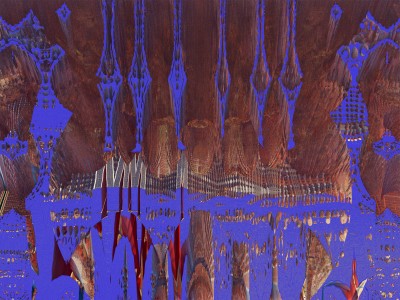
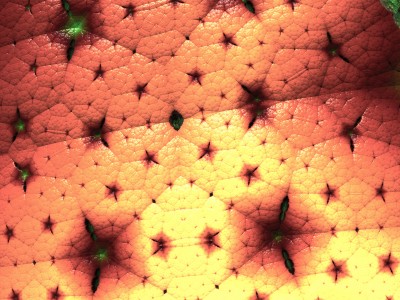
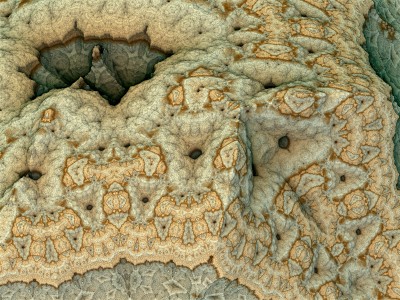
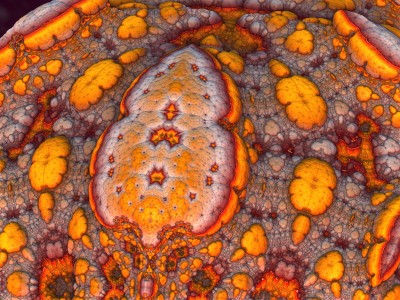
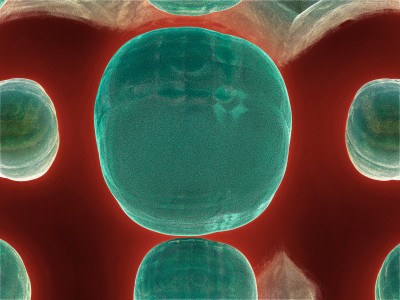
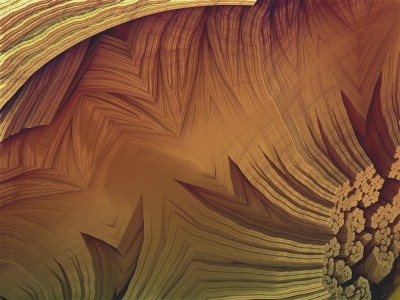
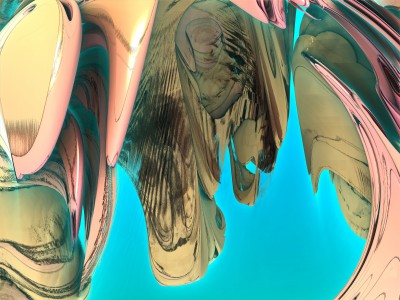
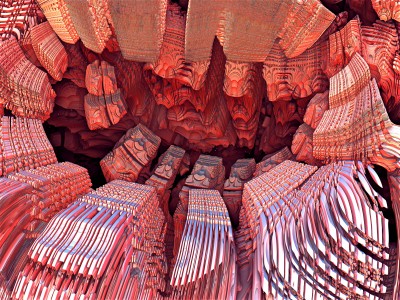
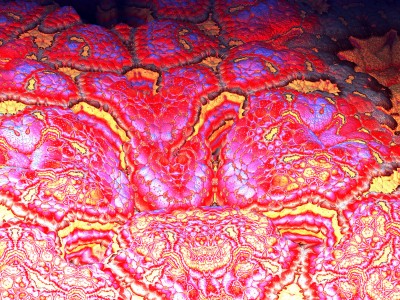
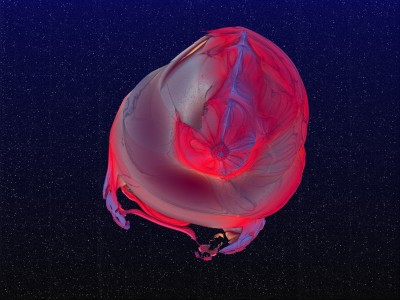
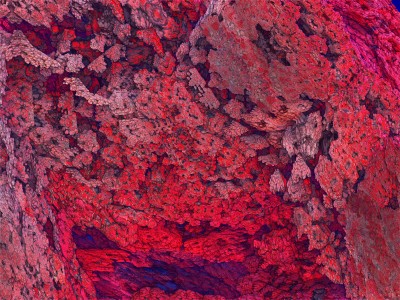
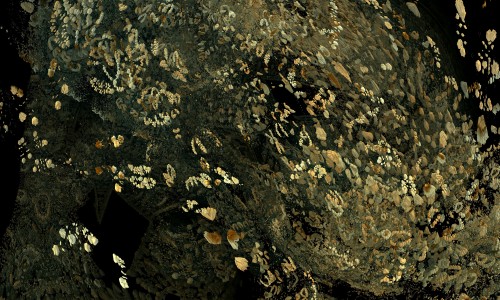
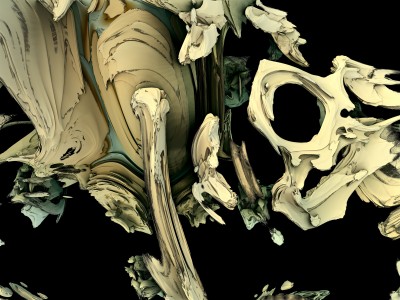
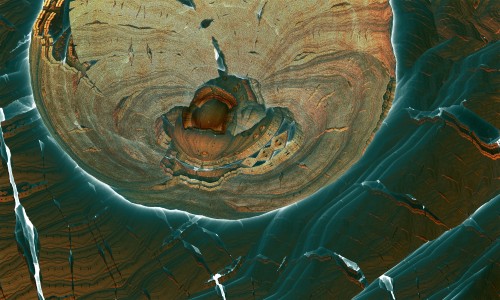
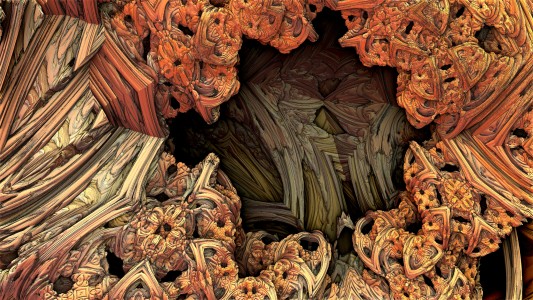
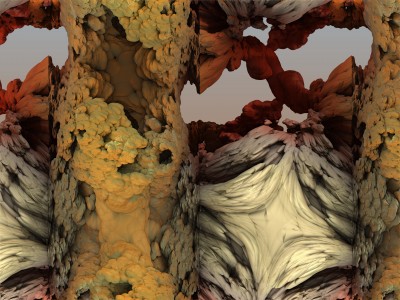
Chaque image est issue d’un calcul fractal : une formule mathématique itérée à l’infini, générant des structures à la fois précises et imprévisibles. Ces formes, modélisées en trois dimensions à l’aide de logiciels libres et de scripts personnalisés, sont ensuite composées comme des paysages improbables, oscillant entre l’organique et le mécanique.
Le titre — µN — condense micro et nombre, soulignant l’échelle paradoxale de ces mondes : infiniment petits dans leur origine numérique, mais potentiellement infinis dans leur déploiement visuel. À l’intérieur de ces espaces, la logique algorithmique rencontre l’aléatoire, produisant des géométries qui semblent vivantes, comme si elles s’auto-engendraient.
Cette série s’inscrit dans une recherche plus large sur les formes génératives, la manipulation des données visuelles et l’esthétique du calcul. Elle questionne notre perception du « réel » en brouillant la frontière entre l’image scientifique, l’artefact numérique et l’œuvre d’art.
Projet de création d’images fractales avec le logiciel Mandelbulb3d, un logiciel gratuit de création d’images fractales 3d, nommé d’après le mathématicien Benoît Mandelbrot, le premier à développer la notion de fractales. Les combinaisons de formules mathématiques offertes par le logiciel sont quasiment infinies, ce qui permet la création d’images très variées.
Séries
Série 10 (juin 2015)
Cliquez sur les images pour visualiser en taille réelle.
Série 9 (avril – mai 2015)
Cliquez sur les images pour visualiser en taille réelle.
Série 8 (mars 2015)
Cliquez sur les images pour visualiser en taille réelle.
Série 7 (février 2015)
Cliquez sur les images pour visualiser en taille réelle.
Série 6 (janvier 2015)
Cliquez sur les images pour visualiser en taille réelle.
Série 5 (décembre 2014)
Cliquez sur les images pour visualiser en taille réelle.
Série 4 (août – novembre 2014)
Cliquez sur les images pour visualiser en taille réelle.
Série 3 (juillet 2014)
Cliquez sur les images pour visualiser en taille réelle.
Série 2 (juin 2014)
Cliquez sur les images pour visualiser en taille réelle.
Série 1 (mai 2014)
Cliquez sur les images pour visualiser en taille réelle.















































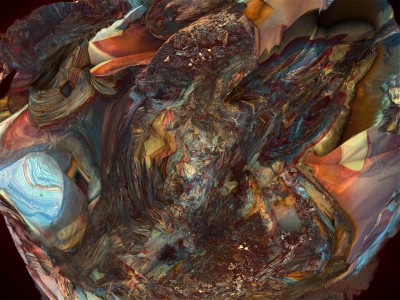




































































































































































Aucun commentaire jusqu'à présent.